Scanning Tunneling Spectroscopy of Insulating Films

Paper for Advanced Solid State Physics class, Dmitri Y. Petrovykh.

Physics Department, University of Wisconsin, Madison, WI, USA (1999)

1. 1 STM and STS of Bulk Insulators
   2 STS of Thin Film Insulators
2. 1 Tunneling Current Theory
   2 Tunneling Barrier Parameters
   3 The Simplest Model for T(E,V)
   4 Thermal Broadening Included
   5 More Accurate Tunneling Probabilities
3. Possible Additional Effects
4. Acknowledgments & References

II.1 Tunneling Current Theory

Since the appearance of the STM most tunneling theories are based on Bardeen's tunneling current formalism⁸, which has been adapted for the STM by Tersoff and Hamann⁹:

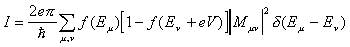
where f(E) is the Fermi function, V - the bias voltage, M_μν—the tunneling matrix element between the states ψ_μ of the tip and ψ_ν of the surface. In special cases M_μν and the whole above expression can be simplified. In a particular case of interest to STS of semiconductors and insulators, we are dealing with the applied bias of the order of 2 eV, which is not small in comparison to kT (0.026 eV at room temperature). For tip-sample bias smaller than a typical work function (4–5 eV) the tunneling current at a fixed location on the surface can be approximated⁶ as:

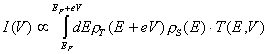
where ρ_T(E+eV) is the density of states of the tip, ρ_S(E) is the density of states of the sample and T(E,V) is the transmission probability of the electron of energy E through the tunneling barrier. Even in this simplified model, a number of assumptions about all the three functions in the integrand can be made to construct more or less realistic models. Several such models will be considered in the following sections.

Top | Home © 1998–2008 Dmitri Petrovykh. Updated 28-Dec-2008.