Scanning Tunneling Spectroscopy of Insulating Films

Paper for Advanced Solid State Physics class, Dmitri Y. Petrovykh.

Physics Department, University of Wisconsin, Madison, WI, USA (1999)

1 STM and STS of Bulk Insulators
2 STS of Thin Film Insulators
1 Tunneling Current Theory
2 Tunneling Barrier Parameters
3 The Simplest Model for T(E,V)
4 Thermal Broadening Included
5 More Accurate Tunneling Probabilities
Possible Additional Effects
Acknowledgments & References

II.4 Thermal Broadening Included via f(E)

The next logical step is to include the effects of the thermal broadening that will be present to some extent at room temperature. It is done by assuming Fermi distribution for the occupied states in both the tip and the sample. That is assume:

ρ_S (E) ~ 1 - f(E)

ρ_T (E) ~ f(E)

f(E) = 1 / (exp[E/kT]+1)

It appears that at this stage the model captures the essence of the process, so it will be examined in some detail. First we should assign realistic values to d_tip and d_ins. In case of CaF₂ (Fig. 2 right curves) the stabilization bias voltage was about 4 V, which corresponds to about 11 Å tip-sample separation. CaF₂ layer grows on top of CaF₁, so if we take CaF₂ layer + the fluorine plane from CaF₁ layer as the insulator, the thickness should be 1¼*3.14 = 3.93 Å. Similarly, for CaF₁ (Fig. 2 left curves) the tip was stabilized at about 3.5 V (d_tip = 10 Å) and the insulator layer thickness is 2.7 Å. Now, the only adjustable parameter in the model is the position of the CBM. Since in this model the peak position coincides with E_CBM, we can set it to 2.3 eV for CaF₁ and 3.7 eV for CaF₂, to match the observed values from Fig. 2. The dI/dV and (dI/dV)/(I/V) curves obtained from this model are presented in Fig. 4. Note the similarity to Fig. 2, even in the absolute values of the normalized conductance. Such similarity is surprising for modeling results with basically no adjustable parameters.

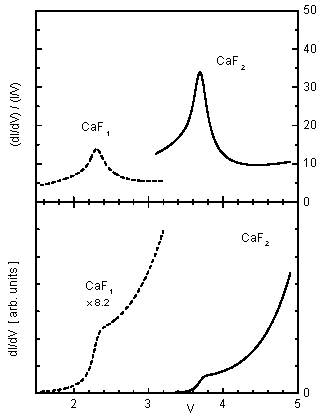
Fig. 4 Calculated tunneling spectra obtained from a minimal model for tunneling through an insulator film. Spectra are shown for CaF₂ and CaF₁, analogous to the data in Fig. 2.

The model also provides some predictions, such as the dependence of the peak height on E_CBM and d_ins. The resonance peak basically scales with both in bilinear fashion:

(dI/dV)/(I/V)_max ~ 2.4 (eV Å)^-1 d_ins E_CBM (see overview in Fig. 5)

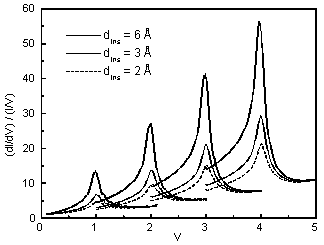
Fig. 5 Peak height dependence on E_CBM and d_ins.

Another very important observation, is that as d_ins tends towards infinity, so does the peak height. As it was pointed out before, in practice there is always the smallest detectable tunneling current limiting our observations for thick (i.e., bulk-like) films, so only a certain range of the normalized conductance will be observed. If the peak height corresponding to a particular film thickness is sufficiently greater than the observable range, than the normalized conductance will appear to have a singularity as it approaches E_CBM (Fig. 6). For E_CBM = 4 eV asymptotic d_ins approaches infinity behavior is reached already for film thickness 15 Monolayers (ML). But finite peaks in the normalized conductance should still be observed for 1-5 ML thick insulator films, with this limiting width decreasing with increasing E_CBM.

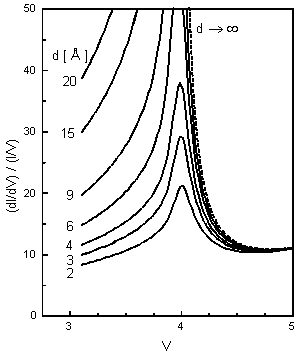
Fig. 6 Apparent singularity in (dI/dV)/(I/V) near E_CBM = 4 eV, as insulator thickness d tends towards infinity.

It is interesting to note that this modeling of the singular behavior seems to be quite universal. In Fig. 7 the model's prediction is compared to the actual data for bulk GaAs. Note that in this case the only adjustable parameter in the model was the value of E_CBM = 1.02 eV, which was assigned in the original paper by Martensson and Feenstra⁷.

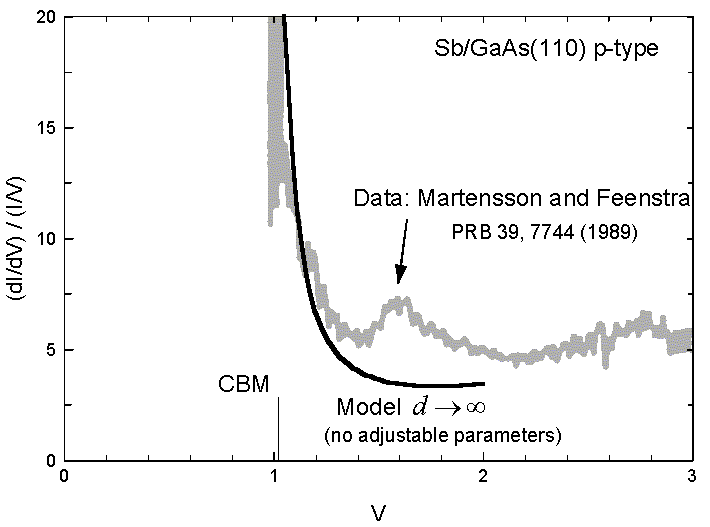
Fig. 7 Normalized conductance singularity near E_CBM. Comparison of the model curve with data for bulk GaAs.

Main page: Chemical contrast STM | Next section: More Accurate Tunneling Probabilities »