Low-Dimensional Surface Structures
One-dimensional Structures
Strictly speaking, one-dimensional (1D) structures are unattainable in the physical world, since unlike lines in mathematics, real objects never quite have zero "height" and "width". However, long objects with very small cross-section can behave approximately like one-dimensional ones. Typically, the requirement is that the cross-section is smaller than the wavelength of electrons in the structure, which means a width of 1–10 nm for metals and semiconductors at room temperature. Quantum mechanics then effectively constrains the "perpendicular" motion of electrons in such a wire and along the wire they behave as if it was one-dimensional.
The smallest physical wire that one can imagine is made of a string of atoms, i.e., is only 1-atom wide. The trick is that for an atomic wire to be one-dimensional, each one of these atoms must be exactly like any other one, which turns out to be difficult to achieve, since such configuration is usually not the lowest energy one because of Peierls distortion.
Theory vs. Experiment
Truly one-dimensional or even quasi one-dimensional structures can serve as a testing ground for our understanding of the way fundamental physics laws scale with dimensionality of the system. For a long time these questions remained primarily in the domain of elegant theoretical problems, since some of the properties for 1D cases can actually be calculated. With the developments in the materials fabrication and characterization experimentalists also became intrigued by the possibility of actually creating low-dimensional systems. In fact 2D electron gases are used in modern devices already. Experimental observation of 1D behavior is more difficult. However, the prospect of seeing predicted exotic phenomena such as Luttinger liquid and spin-charge separation encourages people to keep trying.
Step Decoration
Surfaces and specifically stepped surfaces can be used in a couple of ways to create 1D or at least quasi-1D structures. One approach (image below, left) amounts to making nanowires by step decoration or a similar process. For clear experimental signatures of 1D behavior, these wires preferably should be metallic and "much longer than wider".
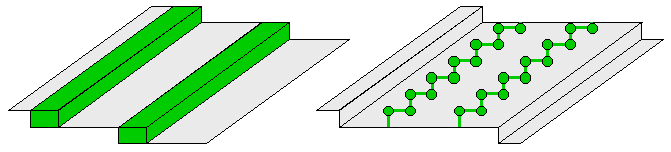
The second approach to creating 1D structures involves anisotropic surface reconstructions (above image, right), which are essentially self-assembled atomic chains.
Surface Anisotropy and Atomic Chains
Quite a few surfaces that exhibit strongly-anisotropic reconstructions have been investigated for signs of 1D behavior. There are, however, a few "show-stoppers" that spoil such attempts in most cases.
Even on well-prepared surfaces often the 1D structures can be oriented along several equivalent directions (domains), thus effectively scrambling any measurement results. Surface steps can break the symmetry of the surface in a well-defined way, thereby providing a single-domain reconstruction.
Second problem with most 1D-candidate structures is their inherent instability with respect to Peierls distortion, which usually destroys the required uniformity along the atomic chains. There is really no way around this effect, so one has to look for systems that are supported by a stable external framework.
Two examples of surface reconstructions that potentially have 1D character are Ca-Si(111)3×1 and Au-Si(111)5×2.
